|
EN BREF
|
La norme d’un vecteur est un concept fondamental en mathématiques, particulièrement en géométrie. Elle représente la longueur d’un vecteur, reliant directement la compréhension de cet objet mathématique à des notions visuelles bien connues. Dans un espace à deux dimensions, la norme peut être calculée à l’aide du théorème de Pythagore, qui fait appel aux coordonnées des points définissant le vecteur. Comprendre la norme permet non seulement d’appréhender la grandeur d’un vecteur, mais aussi d’élargir l’horizon des applications mathématiques, depuis la physique jusqu’à l’informatique.
La norme d’un vecteur est un concept fondamental en mathématiques qui permet de mesurer la longueur d’un vecteur dans un espace donné. Ce terme est souvent rencontré dans la géométrie et l’algèbre linéaire, où il joue un rôle clé dans la compréhension des vecteurs et des opérations qui les concernent. Cet article vise à expliquer la notion de norme, les différentes manières de la calculer et son importance dans divers contextes mathématiques.
Qu’est-ce qu’un vecteur ?
Avant de plonger dans la norme d’un vecteur, il est essentiel de comprendre ce qu’est un vecteur. En mathématiques, un vecteur est un objet qui possède à la fois une grandeur (norme), une direction et un sens. Il est souvent représenté par une flèche, où la longueur de la flèche est proportionnelle à la norme du vecteur. Les vecteurs peuvent être utilisés pour modéliser de nombreuses situations dans la physique, l’ingénierie et d’autres sciences.
La norme d’un vecteur : définition et notation
La norme d’un vecteur, souvent notée ||AB|| pour un vecteur AB, correspond à la longueur de ce vecteur. En d’autres termes, elle mesure la distance entre deux points qui déterminent le vecteur. Ce concept peut être considéré comme une généralisation de la valeur absolue que l’on utilise pour les nombres réels.
Calcul de la norme d’un vecteur en deux dimensions
Pour calculer la norme d’un vecteur dans un plan à deux dimensions (2D), nous appliquons le théorème de Pythagore. Si un vecteur AB a pour coordonnées (x, y), sa norme se calcule à l’aide de la formule suivante :
||AB|| = √(x² + y²)
Cette formule exprime que la norme du vecteur est égale à la racine carrée de la somme des carrés de ses coordonnées. Par exemple, pour un vecteur de coordonnées (3, 4), la norme serait :
||AB|| = √(3² + 4²) = √(9 + 16) = √25 = 5
Calcul de la norme d’un vecteur en trois dimensions
Pour les vecteurs situés dans un espace tridimensionnel (3D), la formule de calcul de la norme est légèrement différente. Si un vecteur AB a pour coordonnées (x, y, z), sa norme se calcule de la manière suivante :
||AB|| = √(x² + y² + z²)
Cette représentation permet de mesurer la longueur du vecteur dans un espace à trois dimensions, ce qui est primordial dans de nombreuses applications, notamment en physique et en ingénierie.
Propriétés de la norme d’un vecteur
La norme d’un vecteur présente plusieurs propriétés intéressantes. Tout d’abord, la norme est toujours positive ou nulle, car elle exprime une distance. De plus, si un vecteur est multiplié par un scalaire k, la norme du nouveau vecteur est proportionnelle à |k|. Par exemple, pour un vecteur u, la norme de k*u est ||k*u|| = |k| * ||u||.
Applications de la norme dans divers domaines
La norme des vecteurs est utilisée dans plusieurs domaines des mathématiques et des sciences. Dans le domaine de la géométrie, elle permet de calculer les distances entre des points. En physique, la norme des vecteurs est utilisée pour quantifier des grandeurs telles que la vitesse, la force et l’accélération. Elle est également essentielle dans le traitement des données informatiques et la modélisation des systèmes dynamiques.
Comprendre la norme d’un vecteur est crucial pour maîtriser divers concepts mathématiques et appliquer ces connaissances dans des situations réelles. Que ce soit dans un cadre académique ou professionnel, la capacité à manipuler et à interpréter des vecteurs et leur norme est une compétence précieuse.
Comparaison des Concepts Liés à la Norme d’un Vecteur
| Concept | Description |
| Norme | Mesure la longueur d’un vecteur dans l’espace. |
| Notation | La norme d’un vecteur AB est notée ||AB||. |
| Formule en 2D | Calculée par la formule √(x² + y²). |
| Théorème utilisé | Basé sur le théorème de Pythagore. |
| Dimension | Peut s’appliquer en 2D, 3D et plus. |
| Applications | Utilisée dans de nombreux domaines comme la physique ou l’informatique. |
| Multiplication par un scalaire | La norme du vecteur 5u est 5 fois la norme de u. |
| Distance entre points | Représente la distance entre deux points définissant le vecteur. |
La norme d’un vecteur est un concept fondamental en mathématiques, souvent compris comme la mesure de sa longueur. Cet article se penche sur la définition de la norme, ses propriétés et les méthodes de calcul, tout en s’appuyant sur le célèbre théorème de Pythagore pour les vecteurs en deux dimensions.
Définition de la norme d’un vecteur
La norme d’un vecteur, notée || AB ||, représente la distance entre deux points définissant un vecteur, souvent appelé segment de droite. Par exemple, dans un espace à deux dimensions, si un vecteur est défini par ses coordonnées (x, y), la norme nous permet de quantifier la longueur de ce vecteur. La norme est une extension de la valeur absolue des nombres, permettant ainsi une approche homogène dans la mesure des grandeurs.
Calcul de la norme d’un vecteur
Pour calculer la norme d’un vecteur en deux dimensions, on utilise la formule suivante :
|| AB || = √(x² + y²)
Cette relation est directement dérivée du théorème de Pythagore, qui établit que dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Cette approche graphique permet de mieux saisir le lien entre les coordonnées d’un vecteur et sa norme.
Propriétés de la norme
La norme présente plusieurs propriétés importantes :
- Positivité : La norme d’un vecteur est toujours positive ou nulle. Un vecteur nul (0) a une norme de 0.
- Homogénéité : Pour tout nombre réel k, la norme d’un vecteur multiplié par ce nombre est k fois la norme originale : || k*u || = |k| * || u ||.
- Inégalité triangulaire : Pour deux vecteurs u et v, la norme de leur somme est toujours inférieure ou égale à la somme de leurs normes : || u + v || ≤ || u || + || v ||.
Applications pratiques de la norme d’un vecteur
Comprendre la norme d’un vecteur est essentiel non seulement en mathématiques mais aussi dans divers domaines comme la physique et l’informatique. Par exemple, en physique, la norme est utilisée pour calculer la distance parcourue par un objet, tandis qu’en informatique, elle joue un rôle crucial dans le traitement de données et la programmation graphique.
Enfin, la norme d’un vecteur est utilisée dans de nombreuses opérations mathématiques avancées et trouve des applications dans des domaines variés tels que l’analyse des données, le traitement d’image et bien d’autres encore.
- Définition : La norme d’un vecteur représente sa longueur.
- Notation : La norme d’un vecteur AB se note ||AB||.
- Représentation : Un vecteur a une grandeur, une direction et un sens.
- Formule : En 2D, la norme est calculée avec √(x² + y²).
- Application : La norme mesure la distance entre deux points qui définissent le vecteur.
- Théorème : Utilisation du théorème de Pythagore pour le calcul de la norme.
- Propriétés : La norme est multiplicative : ||kU|| = |k| * ||U|| pour un nombre réel k.
- Dimensions : En 3D, la norme est donnée par √(x² + y² + z²).
- Importance : Comprendre la norme est essentiel pour des applications pratiques en mathématiques.
Introduction à la norme d’un vecteur
La norme d’un vecteur est un concept fondamental en mathématiques, particulièrement dans le domaine du calcul vectoriel. Elle représente la « longueur » d’un vecteur, permettant ainsi de mesurer sa grandeur. Comprendre comment calculer et interpréter la norme est essentiel pour appréhender divers concepts mathématiques et scientifiques. Dans cet article, nous expliquerons en détail ce qu’est la norme d’un vecteur, comment la calculer en deux dimensions, et son importance dans l’étude des vecteurs.
Qu’est-ce qu’un vecteur ?
Un vecteur est une entité mathématique ayant à la fois une grandeur (ou norme), une direction et un sens. Il peut être représenté graphiquement par une flèche, dont la longueur correspond à la norme et l’orientation indique sa direction. Les vecteurs sont souvent notés par des lettres en gras ou avec une flèche au-dessus des lettres, comme dans le cas du vecteur AB.
La norme d’un vecteur
La norme d’un vecteur, notée ||AB||, est une manière de mesurer sa longueur. En géométrie, elle est définie comme l’extension de la valeur absolue des nombres réels. Cela signifie qu’elle permet de quantifier la distance entre deux points dans un espace donné. Il est important de noter que la norme est toujours une valeur positive, car elle représente une mesure de longueur.
Calcul de la norme en deux dimensions
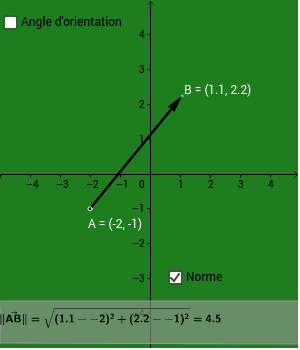
Pour un vecteur situé dans un plan à deux dimensions, représentant les points A (x1, y1) et B (x2, y2), la norme se calcule en appliquant le théorème de Pythagore. La formule est la suivante :
||AB|| = √((x2 – x1)² + (y2 – y1)²)
Cette formule met en évidence que la norme est l’hypoténuse d’un triangle formé par les composants horizontal et vertical du vecteur.
Exemples de calcul de la norme
Pour illustrer le calcul de la norme d’un vecteur, prenons l’exemple du vecteur AB, où A(1, 2) et B(4, 6). En utilisant la formule précédente, nous avons :
||AB|| = √((4 – 1)² + (6 – 2)²) = √(3² + 4²) = √(9 + 16) = √25 = 5
Dans cet exemple, la norme du vecteur AB est égale à 5, représentant ainsi la distance entre les points A et B.
Propriétés de la norme
La norme d’un vecteur possède plusieurs propriétés intéressantes. Par exemple, si nous multiplions un vecteur par un scalaire k (un nombre réel), la norme du nouveau vecteur est :
||k * u|| = |k| * ||u||
Cette propriété indique que multiplier un vecteur par un facteur affecte sa longueur, mais pas sa direction, à condition que le scalaire ne soit pas nul.
Importance de la norme dans les applications
La norme d’un vecteur est non seulement une notion théorique, mais elle a également de nombreuses applications pratiques. Elle est utilisée dans la physique pour mesurer des forces, dans l’informatique pour des algorithmes de recherche de similarité et dans diverses branches de l’ingénierie. Comprendre la norme est donc crucial pour toute personne travaillant avec des vecteurs dans différents contextes scientifiques et techniques.